Les régressions sont généralement les premiers algorithmes de modélisation utilisés pour l’apprentissage automatique et la science des données. Ces méthodes sont excellentes car elles sont faciles à utiliser et à interpréter. Cependant, leur simplicité inhérente présente également quelques inconvénients et dans de nombreux cas, ils ne constituent pas vraiment le meilleur choix du modèle de régression. Il existe en fait plusieurs types de régressions, chacune avec ses avantages et ses inconvénients.
Dans cet article, nous allons examiner 5 des algorithmes de régression les plus courants et leurs propriétés. Nous verrons que beaucoup d’entre eux sont enclins à bien fonctionner dans certaines situations et avec certains types de données. Cet article vous donnera quelques outils supplémentaires dans votre boîte à outils de régression et vous donnera une meilleure idée des modèles de régression dans leur ensemble.
La Régression linéaire
C’est l’une des techniques de modélisation les plus connues. La régression linéaire fait généralement partie des premiers sujets choisis par les participants lors de l’apprentissage de la modélisation prédictive. Dans cette technique, la variable dépendante est continue, la ou les variables indépendantes peuvent être continues ou discrètes et la nature de la droite de régression est linéaire.
La régression linéaire établit une relation entre la variable dépendante Y et une ou plusieurs variables indépendantes X en utilisant une droite de meilleur ajustement (également appelée ligne de régression).
Il est représenté par une équation Y = a + b * X + c, où a est intercept, b est la pente de la ligne et c est un terme d’erreur. Cette équation peut être utilisée pour prédire la valeur de la variable cible en fonction de variables prédictives données.
La différence entre la régression linéaire simple et la régression linéaire multiple réside dans le fait que la régression linéaire multiple a plusieurs variables indépendantes, alors que la régression linéaire simple ne comporte qu’une variable indépendante. On peut ecrire l’equation de regression lineaire multiple ainsi : Y = a + b1 * X1 + b2 * X2 +…+ bn * Xn + c .
Quelques points clés sur la régression linéaire:
- Rapide et facile à modéliser
- Très intuitive et facile à comprendre et à interpréter
- La régression linéaire est très sensible aux valeurs aberrantes
La Régression Polynomiale
Quand nous voulons concevoir un modèle adapté à la gestion de données non linéairement disposées, nous devons utiliser une régression polynomiale. Pour cette méthode de régression, la meilleure courbe n’est pas une droite. C’est plutôt une courbe qui s’inscrit dans les points de données. Pour une régression polynomiale, la puissance de certaines variables indépendantes est supérieure à 1.
- Y = an·xn + an – 1·xn-1 + … + a1·xn-1 + a0·x0
Nous pouvons avoir certaines variables ayant des exposants, d’autres sans, et également sélectionner l’exposant exact que nous voulons pour chaque variable. Cependant, la sélection de l’exposant exact de chaque variable nécessite naturellement une certaine connaissance du lien entre les données et la sortie.
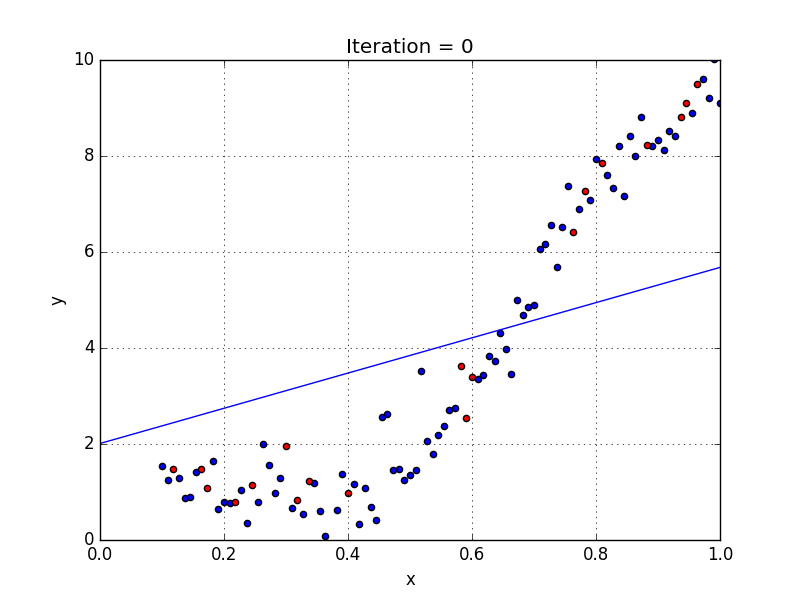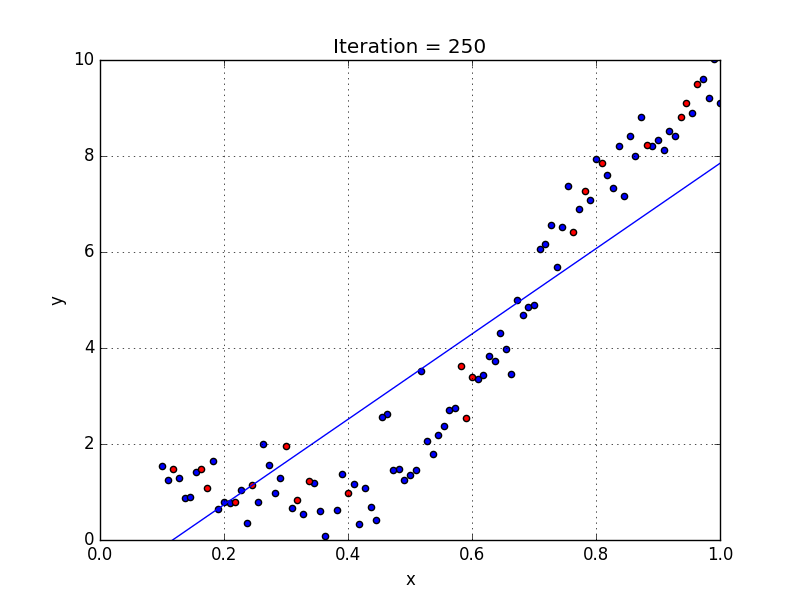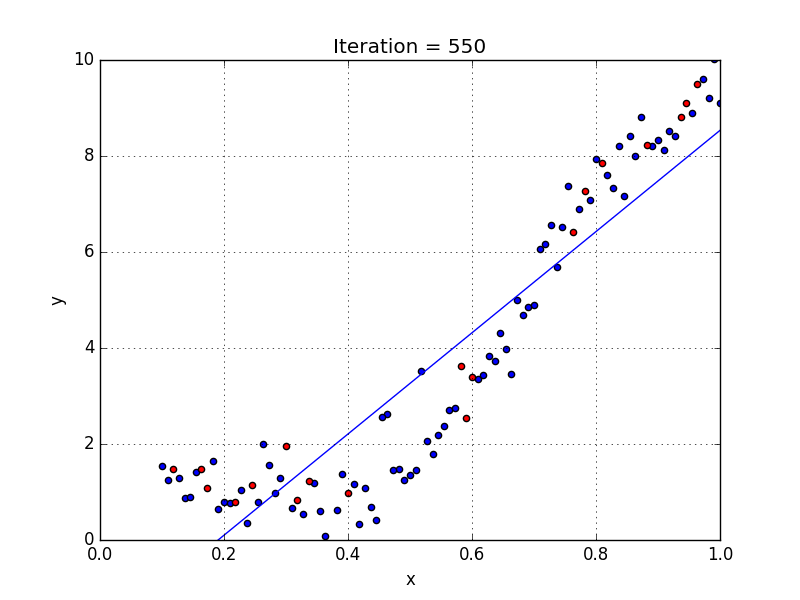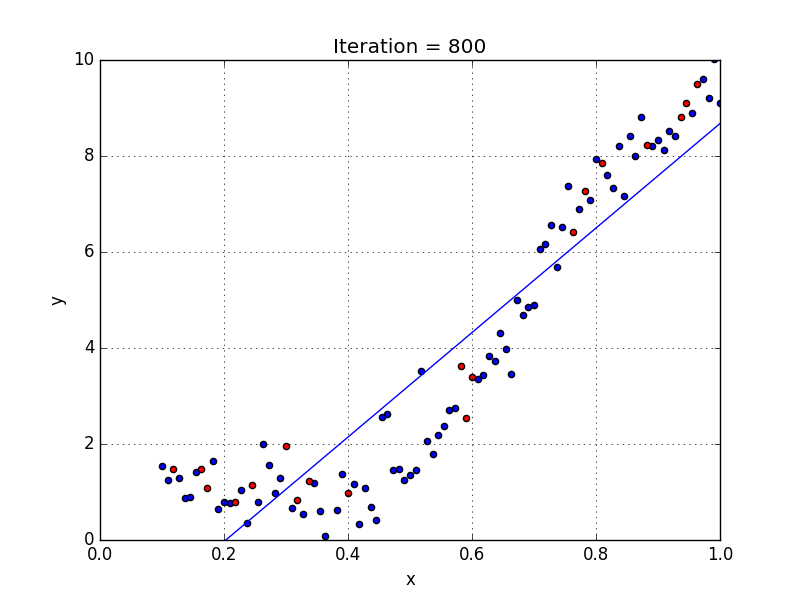
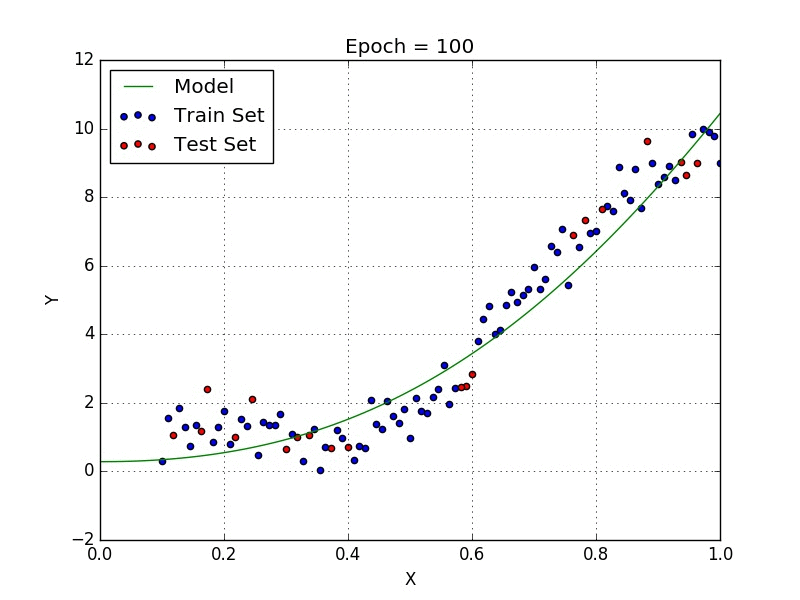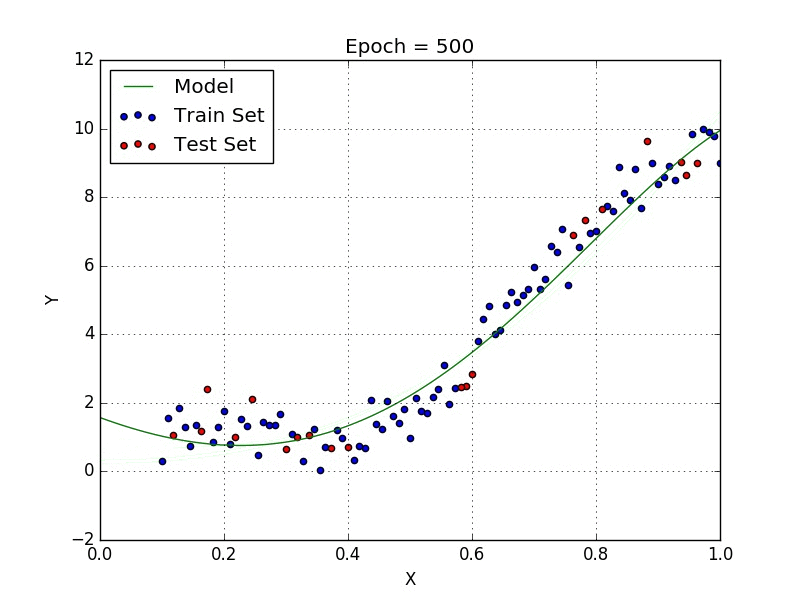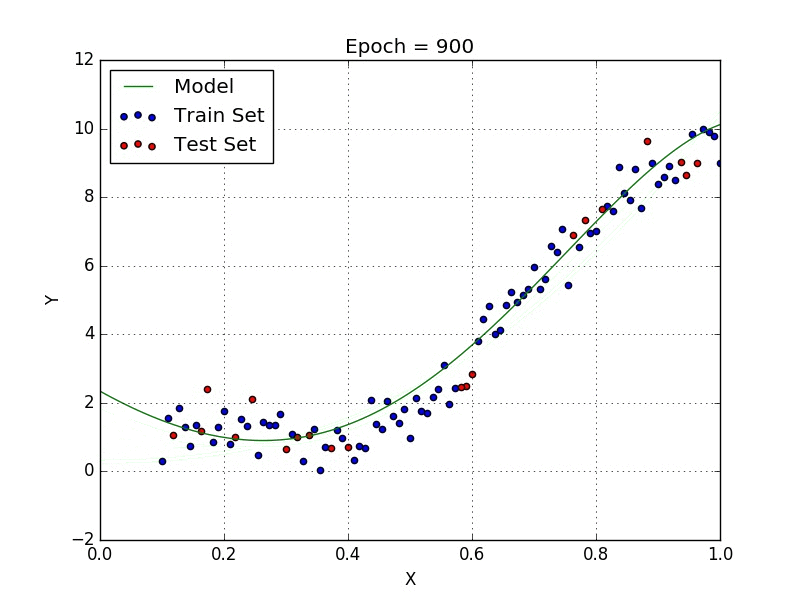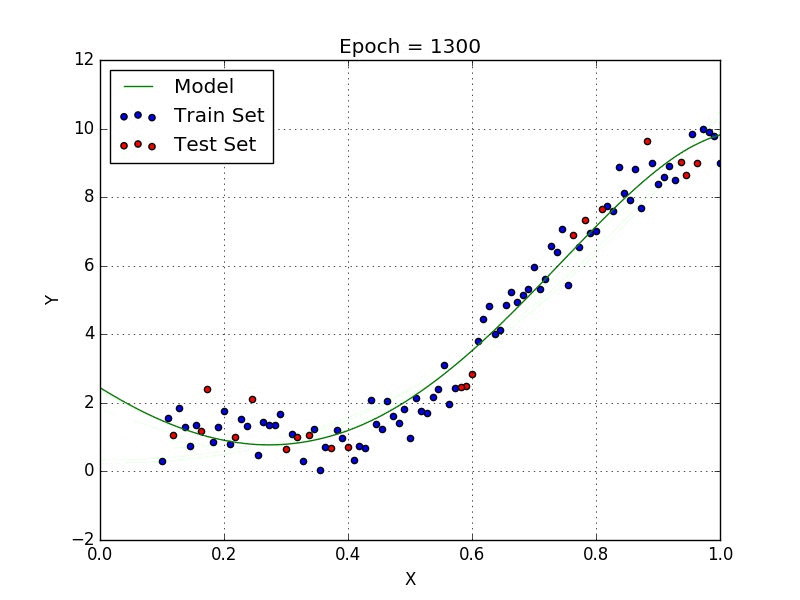
Quelques points clés sur la régression polynomiale:
- Capable de modéliser des données non linéaires
- Contrôle sur la modélisation des variables de caractéristiques
- Nécessite d’une connaissance des données afin de sélectionner les meilleurs exposants.
- Sujet à un overfitter si les exposants sont mal sélectionnés
La Régression Logistique
La régression logistique est utilisée pour trouver la probabilité d’un événement. On veut determiner le succès ou l’échec d’un événement. On utilise la régression logistique lorsque la variable dépendante est de en semble de valeurs fini (0/1, Vrai / Faux, Oui / Non). Ici, la valeur de Y va de 0 à 1.
Les points importants:
- Est largement utilisé pour les problèmes de classification
- Ne nécessite pas de relation linéaire entre les variables dépendantes et indépendantes
- Peut gérer différents types de relations
- Pour éviter l’overfitting et les underfitting, il est preferable d’inclure toutes les variables significatives.
- Nécessite des échantillons de grande taille car les estimations du maximum de vraisemblance sont moins puissantes pour les échantillons de faible taille
- Les variables indépendantes ne doivent pas être corrélées les unes avec les autres
- Si la valeur de la variable dépendante est ordinale, elle est appelée régression logistique ordinale.
- Si la variable dépendante est multi-classe, elle est appelée régression logistique multinomiale.
La Régression de Crête
La régression de crête est une technique d’analyse de données de régression multiples avec multicolinéarité. Lorsque la multicollinéarité est avérée, les estimations des moindres carrés sont sans biais, mais leurs variances étant importantes, elles peuvent être loin de la valeur réelle. En ajoutant un degré de biais aux estimations de régression, la régression de crête réduit les erreurs standard. On espère que l’effet net sera de donner des estimations plus fiables.
Quelques points clés sur Ridge Regression:
- Les hypothèses de cette régression sont identiques à celles de la régression par le moindre carré, sauf que la normalité ne doit pas être présumée.
- Il réduit la valeur des coefficients mais n’atteint pas zéro, ce qui suggère qu’aucune fonctionnalité de sélection d’entités
La Régression Lasso
Le lasso (opérateur de sélection et de retrait le plus absolu) pénalise la taille absolue des coefficients de régression. De plus, il est capable de réduire la variabilité et d’augmenter la précision des modèles de régression linéaire.
La régression de Lasso, diffère de la régression de crête en ce sens qu’elle utilise des valeurs absolues dans la fonction de pénalité, au lieu de carrés. Cela conduit à des valeurs pénalisantes ce qui a pour effet de rendre certaines estimations de paramètres parfaitement nulles. Plus la sanction appliquée est importante, plus les estimations sont ramenées au zéro absolu. Cela résulte en une sélection de variables sur n variables.
Les points importants:
- Les hypothèses de cette régression sont les mêmes que la régression par le moindre carré, sauf que la normalité ne doit pas être présumée
- Il réduit les coefficients à zéro (exactement zéro), ce qui aide certainement dans la sélection des fonctionnalités
- Ceci est une méthode de régularisation et utilise la régularisation l1
Si le groupe de prédicteurs est fortement corrélé, le lasso n’en sélectionne qu’un et ramène les autres à zéro