Les mathématiques représentent la base de toute discipline scientifique. Presque tous les concepts de Data Science et Machine Learning reposent sur des bases mathématiques.
Dans votre apprentissage des techniques, algorithmes et langages de programmation en vue de devenir Data Scientist ou d’approfondir vos connaissance, il ne faut pas OUBLIER les mathématiques.
Il est souvent préférable de connaitre les dessous des algorithmes que vous utiliserez que d’être un simple exécutant. Par conséquent, une solide compréhension des mathématique vous donnera un avantage concurrentiel parmi vos pairs.
Considérons un développeur ou un analyste. Ils peuvent traiter un grand nombre de données et d’informations, mais ils sont pas intéressés par une modélisation de ces données. Souvent, l’accent est mis sur l’utilisation des données pour un besoin immédiat plutôt que sur une exploration scientifique approfondie.
La Data Science, en revanche, devrait s’intéresser aux modèles et ainsi suivre un processus scientifique. Le processus scientifique est le suivant :
- Modéliser un processus en sondant la dynamique sous-jacente
- Construire des hypothèses
- Mesurer la qualité de la source de données
- Quantifier l’incertitude
- Identifier le modèle caché à partir des données analysées
- Comprendre les limites du modèle
La Data Science est applicable à, presque, tous les domaines. Ainsi, elle peut traiter des problèmes aussi divers que le diagnostic du cancer et l’analyse du comportement social.
Cela donne la possibilité d’un tableau vertigineux d’objets mathématiques à n dimensions, de distributions statistiques, de fonctions d’optimisation, etc.
Dans le reste de l’article, je vous fourni les notions qu’il faut maitriser pour faire partie des meilleurs Data Scientists.
Fonctions, variables, équations et graphiques
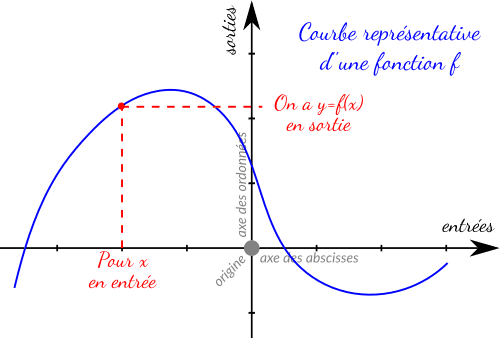
Fonction Mathématique
Cette partie couvre les bases mathématiques, de l’équation au théorème binomial :
- Logarithme, fonctions exponentielles, fonctions polynomiales, nombres rationnels
- Géométrie, identités trigonométriques
- Inégalités
- Nombres réels et complexes, propriétés de base
- Graphique, coordonnées cartésiennes et polaires
- Séries, suites
Cas d’utilisation
Si vous souhaitez comprendre comment une requête s’exécute rapidement dans une base de données contenant des données massives triée, vous rencontrerez le concept de «recherche binaire».
Pour en comprendre ce concept, vous devez comprendre les logarithmes et la récurrence.
Ou, si vous souhaitez analyser une série temporelle, vous pouvez rencontrer des concepts tels que «fonctions périodiques».
Statistiques

Statistiques
Apprendre et maîtriser les concepts statistique et probabiliste est un pré-requis quand on parle de Machine Learning. Chaque Data Scientist doit avoir de solide connaissance en statistique.
De nombreux Data Scientists considèrent en fait que le Machine Learning n’est qu’un apprentissage statistique.
Bien évidement c’est un sujet très vaste et une planification et organisation sont essentielles pour couvrir les concepts les plus importants :
- Statistiques descriptives, variance, covariance, corrélation
- Probabilité de base, espérance, calcul de probabilité, théorème de Bayes, probabilité conditionnelle
- Fonctions de distribution de probabilité
- Échantillonnage, mesure, erreur, génération de nombres aléatoires
- Tests d’hypothèses, tests A / B, intervalles de confiance, valeurs p
- ANOVA, test t
- Régression linéaire, régularisation
Mathématiques discrètes

Mathématiques discrètes
Les Mathématiques discrètes sont rarement cité quand on parle de Data Science. Et pourtant les mathématiques discrètes sont au cœur des systèmes informatiques modernes.
Vous devez connaitre les concepts de Maths discrète d’algorithmes et de structures de données dans un projet d’analyse :
- Ensembles, sous-ensembles, ensembles d’alimentation
- Fonctions de comptage, combinatoire, comptabilité
- Techniques de preuve de base: induction, preuve par contradiction
- Bases de la logique inductive, déductive et propositionnelle
- Structures de données de base: piles, files d’attente, graphiques, tableaux, tables de hachage, arbres
- Propriétés du graphique: composants connectés, degré, concepts de débit maximal / minimum de coupe, coloration du graphique
- Relations de récurrence et équations
- Croissance des fonctions et concept de notation O (n)
Algèbre linéaire
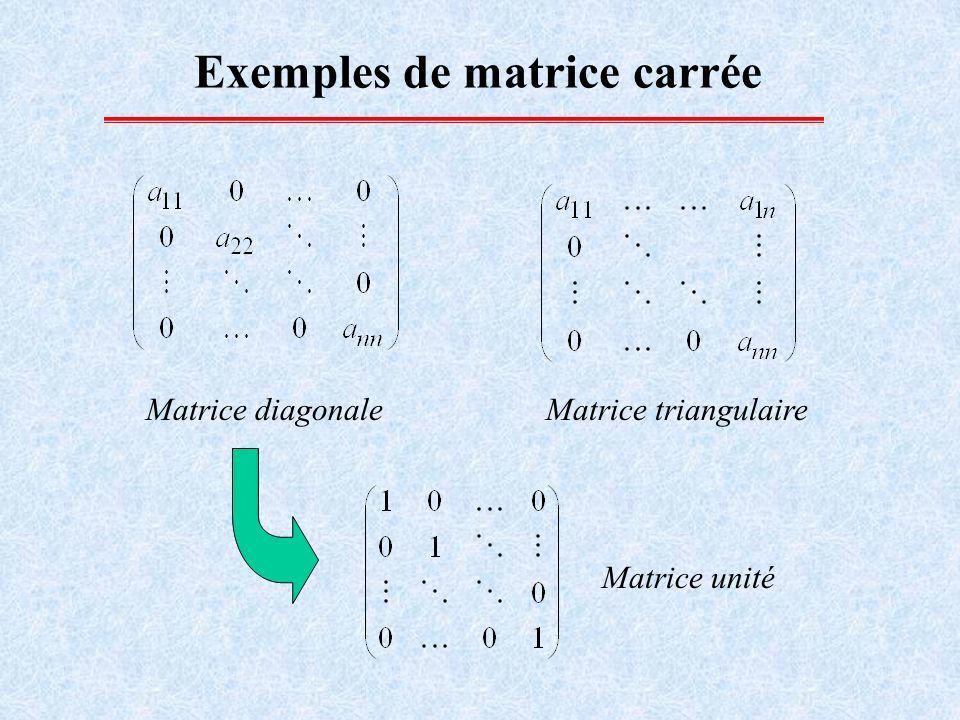
Algèbre linéaire
Pour comprendre le fonctionnement des algorithmes de Machine Learning sur un flux de données afin de créer un aperçu, l’algèbre linéaire est essentielle.
Vous avez certainement déjà eu des suggestions d’amis sur Facebook ou des recommandations de video sur YouTube, en passant par le transfert de votre selfie vers un portrait à la Salvador Dali utilisant l’apprentissage par transfert en profondeur. Tous ces exemples implique des matrices et une algèbre matricielle.
Les notions que vous devez apprendre :
- Propriétés de base de la matrice et des vecteurs: multiplication scalaire, transformation linéaire, transposition, conjugaison, rang, déterminant
- Produits internes et externes, règle de multiplication de matrice et divers algorithmes, matrice inverse
- Concept de factorisation matricielle / décomposition de LU, élimination de Gauss / Gauss-Jordan, résolution du système d’équation linéaire Ax = b
- Matrices spéciales: matrices carrées, matrices d’identité, matrices triangulaires, idées sur les matrices creuses et denses, vecteurs unitaires, matrices symétriques, matrices hermitiennes, asymétriques et unitaires
- Valeurs propres, vecteurs propres, diagonalisation, décomposition en valeurs singulières
- Espace vectoriel, base, étendue, orthogonalité, orthonormalité, moindre carré linéaire
Cas d’utilisation
- Pour faire une analyse en composantes principales on utilise la décomposition en valeurs singulières pour obtenir une représentation de dimension compacte du jeu de données avec moins de paramètres.
- Les algorithmes de réseau de neurone utilisent des techniques d’algèbre linéaire pour représenter et traiter les structures de réseau et les opérations d’apprentissage.
Calcul
Calculs
Le calcul apparaît partout en Data Science et en apprentissage automatique et plus globalement derrière tous les programmes et algorithmes.
Les calculs se cachent derrière la solution analytique d’apparence simple d’un problème des moindres carrés ordinaires en régression linéaire ou intégrée à chaque propagation en retour de votre réseau de neurones pour apprendre un nouveau motif.
Si vous deviez vos concentrer que sur les concepts essentielles, apprenez ces sujets :
- Fonctions de variable unique, limite, continuité, différentiabilité
- Théorèmes de valeur moyenne, formes indéterminées, règle de L’Hospital
- Maxima et minima
- Produit et chaîne règle
- Série de Taylor, concepts de sommation / intégration de séries infinies
- Théorèmes fondamentaux et de valeur moyenne du calcul intégral, évaluation d’intégrales définies et impropres
- Fonctions bêta et gamma
- Fonctions de variables multiples, limite, continuité, dérivées partielles
- Bases des équations différentielles ordinaires et partielles
Thèmes d’optimisation et de recherche opérationnelle
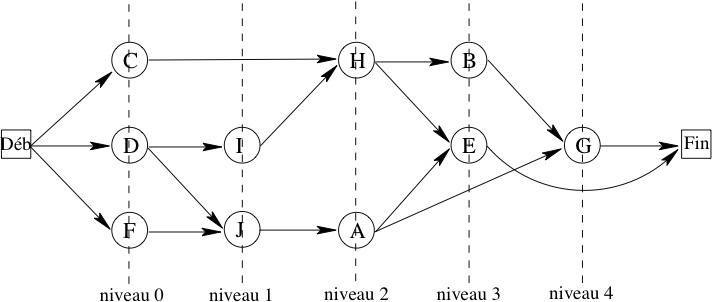
recherche opérationnelle
Ces concepts sont très pertinents car une compréhension de base de ces techniques puissantes peut être fructueuse dans la pratique du Machine Learning.
Pratiquement tous les algorithmes de Machine Learning visent à minimiser un type d’erreur d’estimation soumis à diverses contraintes, ce qui constitue un problème d’optimisation.
Vous devez à minima vous intéresser à ces sujets:
- Bases de l’optimisation
- Formuler le problème d’optimisation
- Maxima, minima, fonction convexe, solution globale
- Techniques d’optimisation randomisée: escalade, recuit simulé, algorithmes génétiques
- Programmation linéaire, programmation entière
- Programmation par contraintes, problème de sac à dos